Trenuj! – ciągi część 1

Przed nami kilka zadań treningowych pochodzących z arkuszy CKE. Czym są ciągi, a w szczególności ciąg arytmetyczny i geometryczny? Jeśli jeszcze nie wiesz zajrzyj tutaj.

Rozwiązanie:

Sposób I:
Mamy dane $a_1=3, a_9=12$ .
Szukamy $a_5$ , piątego wyrazu ciągu geometrycznego, czyli $a_5=a_1\cdot q^4$ .
Zauważmy, że

$\frac{a_9}{a_1}=\frac{a_1\cdot q^8}{a_1}=q^8$

Zatem $q^8=\frac{12}{3}=4$ . Stąd $q^4=\sqrt {q^8}=\sqrt 4=2$
$a_5=a_1\cdot q^4=3\cdot 2 =6$
Odpowiedź B.

Sposób II:
Możemy zauważyć, że piąty wyraz ciągu jest średnią geometryczną pierwszego i dziewiątego wyrazu ciągu:

$a_1,...,...,...,a_5,...,...,...,a_9$

Zatem

$a_5=\sqrt {a_1\cdot a_9}=\sqrt {3\cdot 12}=\sqrt {36}=6$

Rozwiązanie:

Sprawdźmy kiedy $a_n<0$
Rozwiązaniem nierówności $(n+3)(n-5)<0$ jest zbiór $(3,5)$ , po uwzględnieniu $n\ge 1$ mamy rozwiązanie $n\in \{1,2,3,4\}$
(Jeśli nie pamiętasz, jak rozwiązać nierówność kwadratową koniecznie zajrzyj tutaj.)
Sprawdźmy to:
$a_1=(1+3)(1-5)=4\cdot (-4)<0$
$a_2=(2+3)(2-5)=5\cdot (-3)<0$
$a_3=(3+3)(3-5)=9\cdot (-2)<0$
$a_4=(4+3)(4-5)=7\cdot (-1)<0$
$a_5=(5+3)(5-5)=8\cdot 0=0$
$a_6=(6+3)(6-5)=9\cdot 1>0$
Kolejne wyrazy ciągu będą liczbami dodatnimi.
Odpowiedź B.

Rozwiązanie:

Jeśli liczby $x-2,6,12$ są kolejnymi wyrazami ciągu geometrycznego, to iloraz pierwszej i drugiej jest taki sam, jak iloraz drugiej i trzeciej. Możemy użyć zapisu:

$\frac{6}{x-2}=\frac{12}{6}$

Wówczas mamy:

$12\cdot (x-2)=6\cdot 6\ |:12$

$x-2=\frac{36}{12}$

$x-2=3$

$x=5$

Odpowiedź D.

Rozwiązanie:

$n=?$
Skorzystajmy ze wzoru ogólnego dla ciągu arytmetycznego

$a_n=a_1+(n-1)\cdot r$

Wiemy, że $a_1=-4, r=2$ . Zatem:

$156=-4+(n-1)\cdot 2$

$156=-4+2n-2$

$156+6=2n$

$2n=162\ |:2$

$n=81$

Odpowiedź A.

Rozwiązanie:

Mamy do czynienia z ciągiem geometrycznym. Wykorzystamy wzór ogólny $a_n=a_1\cdot q^{n-1}$
Wiemy, że

$a_4=3\cdot a_1$

zatem

$a_1\cdot q^3=3\cdot a_1$

$q^3=3$

$q=\sqrt [3]3$

Odpowiedź C.

Przejdźmy do zadań otwartych. Na początek, coś, co na pierwszy rzut (niewprawnego) oka wcale nie wygląda jak ciągi. Ale jednak!

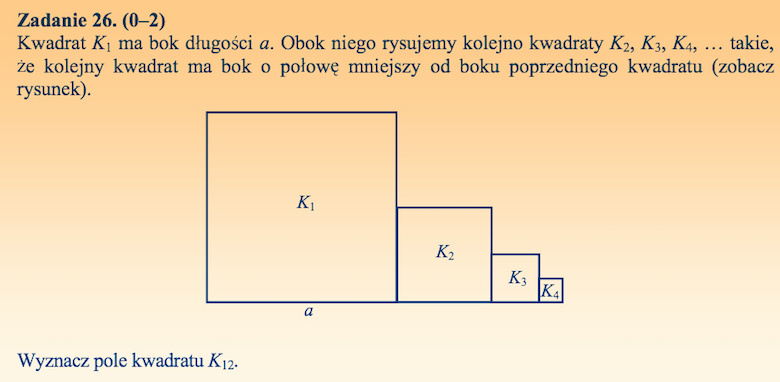
Rozwiązanie:

Kolejne kwadraty mają boki długości

$a,\ \frac{1}{2}a,\ \frac{1}{4}a,\ \frac{1}{8}a,\ ....$

Zatem ich pola można zapisać za pomocą wyrażeń:

$a^2,\biggl(\frac{1}{2}a\biggr)^2,\biggl(\frac{1}{4}a\biggr)^2,\biggl(\frac{1}{8}a\biggr)^2,....$

czyli

$a^2,\ \frac{1}{4}a^2,\ \frac{1}{16}a^2,\ \frac{1}{64}a^2,\ ....$

Zauważmy, że pola kwadratów tworzą ciąg geometryczny taki, że $a_1=a^2, q=\frac{1}{4}$ .
Zatem nasz szukany dwunasty wyraz tego ciągu (czyli pole kwadratu $K_{12}$ ) wygląda następująco:

$a_{12}=a_1\cdot q^{11}=\frac{1}{4^{11}}\cdot a^2=\frac{1}{4\ 194\ 304}\ a^2$

A teraz zadanie otwarte, za które w majowej sesji egzaminacyjnej w 2015 roku można było zdobyć aż 5 punktów! Czyli aż 10%! (marzenie wielu). Polecam wnikliwą analizę rozwiązania.

Rozwiązanie:

Wiemy, że $S_{11}=187$ , czyli $\frac{a_1+a_{11}}{2}\cdot 11=187$

oraz $\frac{a_1+a_3+a_9}{3}=12$ , stąd – wykorzystując wzór ogólny – mamy: $\frac{a_1+a_1+2r+a_1+8r}{3}=12$

co daje $a_1+a_1+2r+a_1+8r=36$ . Zatem

$3a_1+10r=36$

Wróćmy do sumy jedenastu początkowych wyrazów tego ciągu:

$\frac{a_1+a_{11}}{2}\cdot 11=187$

$\frac{a_1+a_1+10r}{2}\cdot 11=187\ |:11$

$\frac{2a_1+10r}{2}=17\ |\cdot 2$

$2a_1+10r=34$

Zbierzmy wszystko, co mamy:

$\begin {cases} 3a_1+10r=36\\ 2a_1+10r=34\end{cases}$

Rozwiążemy układ równań metodą przeciwnych współczynników. Pomnóżmy drugie z równań przez $-1$ , a otrzymamy:

$\begin {cases} 3a_1+10r=36\\ -2a_1-10r=-34\end{cases}$

Dodajemy równania i otrzymujemy:

$\begin {cases} a_1=2\\ 3a_1+10r=36\end{cases}$

Skorzystajmy z podstawienia $a_1=2$

$\begin {cases} a_1=2\\ 3\cdot 2+10r=36\end{cases}$

$\begin {cases} a_1=2\\ 10r=36-6\end{cases}$

$\begin {cases} a_1=2\\ r=3\end{cases}$

W ten sposób wyznaczyliśmy ciąg arytmetyczny. Szczególnie interesują nas wyrazy $a_1, a_3, a_k$ tego ciągu.
$a_1=2$ to już wiemy
$a_3=?$
Skorzystajmy ze wzoru ogólnego $a_3=a_1+2r=2+2\cdot 3=8$ .
Z kolei $a_k=a_1+(k-1)\cdot r=2+(k-1)\cdot 2=2+3k-3=3k-1$

Wróćmy do naszych szukanych.

$a_1,a_3,a_k$

Ile wynosi $k$ ?

$a_1,a_3,a_k$ to kolejne wyrazy (nowego) ciągu geometrycznego – ich iloraz jest stały. Zatem liczby te spełniają warunek:

$\frac{a_3}{a_1}=\frac{a_k}{a_3}$

czyli

$\frac{8}{2}=\frac{3k-1}{8}$

zatem

$2\cdot (3k-1)=8\cdot 8$

stąd

$6k-2=64$

$6k=66$

Odpowiedź:

$k=11$

WNIOSKI:
1. Istnieje wiele sposobów na rozwiązanie zadania. Nie ma jednego właściwego. Prezentowany wybór rozwiązań jest subiektywny.
2. Ciągi naprawdę nie są skomplikowane, dlatego warto poświęcić im dłuższą chwilę, gdyż podczas egzaminu maturalnego można zdobyć za same zadania z ciągów od 4 do 14%.

O MATHko!

Trenuj! – ciągi część 1

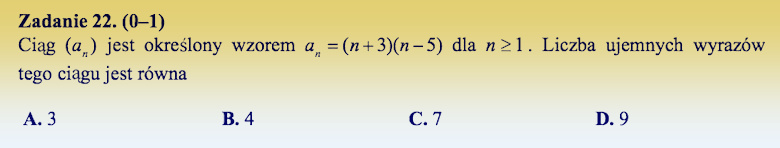
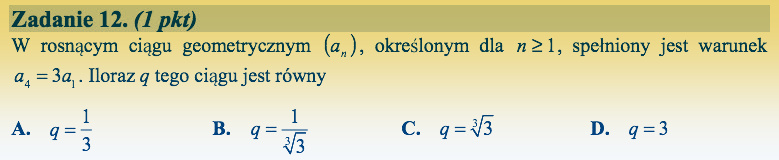
Dodaj komentarz Anuluj pisanie odpowiedzi