Trenuj! – trygonometria cz. 1

Zaczynamy trening od zadań zamkniętych z arkuszy CKE. Poziom trudności będzie wzrastał.

Rozwiązanie:

Tutaj główna trudność polega na odczytaniu wartości funkcji dla odpowiedniego kąta, podstawieniu i wykonaniu odpowiedniego wyliczenia. (Pamiętaj o wspólnym mianowniku podczas odejmowania ułamków.)

$tg30^\circ=\frac{\sqrt 3}{3}$

$sin30^\circ=\frac{1}{2}$

Zatem

$tg30^\circ -sin30^\circ=\frac{\sqrt 3}{3}-\frac{1}{2}=\frac{2\sqrt 3}{6}-\frac{3}{6}=\frac{2\sqrt 3 -3}{6}=\frac{2\sqrt 3-3}{6}$

Odpowiedź D.

200115

Rozwiązanie:

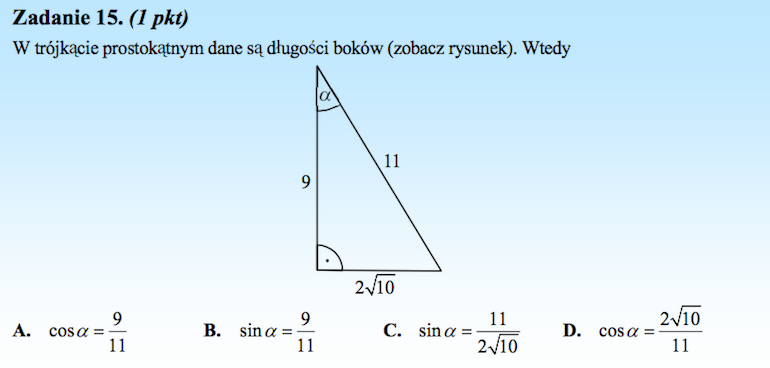
Przypomnijmy, że sinus kąta wyraża zależność między długością przyprostokątnej leżącej naprzeciw kąta do długości przeciwprostokątnej. Zatem dla naszego trójkąta

$\sin\alpha=\frac{2\sqrt{10}}{11}$

Cosinus kąta to zależność między długościami przyprostokątnej leżącej przy kącie $\alpha$ oraz przeciwprostokątnej. (Tak – te informacje można znaleźć, ewentualnie sprawdzić dla pewności, w tablicach.)

$\cos\alpha=\frac{9}{11}$

Odpowiedź A.

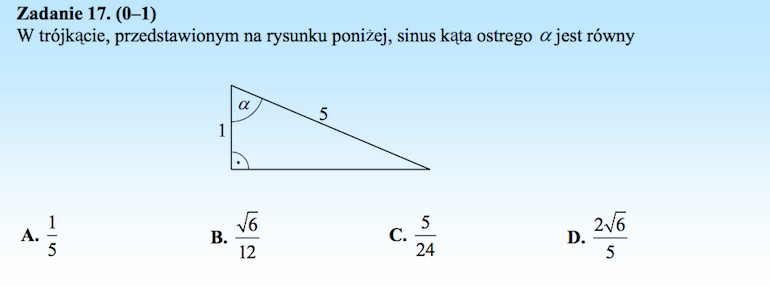
Rozwiązanie:

(Sprawdź definicję sinusa we wcześniejszym zadaniu.) Do wyznaczenia tej zależności potrzebujemy długości przyprostokątnej leżącej naprzeciw kąta $\alpha$ .

$\sin\alpha=\frac{x}{5}$

Z twierdzenia Pitagorasa mamy

$1^2+x^2=5^2$

$x^2=25-1$

$x=\sqrt{24}$

$x=\sqrt{4\cdot 6}=\sqrt4\cdot\sqrt6=2\sqrt6$

Zatem

$\sin\alpha=\frac{2\sqrt6}{5}$

Odpowiedź D.

Rozwiązanie:

Skorzystajmy ze wzoru:

$sin^2\alpha+cos^2\alpha=1$

Inne wzory znajdziesz tutaj.
Wówczas

$cos^2\alpha=1-sin^2\alpha$

Zatem

$cos^2\alpha=1-\bigg(\frac{\sqrt3}{2}\bigg)^2=1-\frac{3}{4}=\frac{1}{4}$

Stąd

$cos^2\alpha-2=\frac{1}{4}-2=-\frac{7}{4}$

Odpowiedź A.

Rozwiązanie:

Szukamy w tabeli wartości funkcji trygonometrycznych kąta, dla którego $tg\ \alpha=1$ .
Odpowiedź C.

Rozwiązanie:

Skorzystajmy z faktu

$tg\ \alpha=\frac{sin\ \alpha}{cos\ \alpha}$

Wówczas

$\frac{sin\ \alpha}{cos\ \alpha}=2sin\ \alpha\ |:sin\alpha$

Możemy dzielić, gdyż dla danych wartości kąta $sin\ \alpha$ jest różny od zera.

$\frac{1}{cos\ \alpha}=2$

$1=2\cdot cos\ \alpha\ |:2$

$cos\ \alpha=\frac{1}{2}$

Odpowiedź A.

Rozwiązanie:

Skorzystajmy z jedynki trygonometrycznej:

$sin^2\alpha+cos^2\alpha=1$

Zatem

$sin^2\alpha=1-cos^2\alpha$

Stąd i z faktu, że $\alpha$ jest kątem ostrym mamy:

$sin\ \alpha=\sqrt{1-cos^2\alpha}=\sqrt{1-\bigg(\frac{5}{13}\bigg)^2}= \sqrt{1-\frac{25}{169}}=\sqrt{\frac{169}{169}-\frac{25}{169}}=\sqrt{\frac{144}{169}}=\frac{12}{13}$

Przypomnijmy, że

$tg\ \alpha=\frac{sin\ \alpha}{cos\ \alpha}$

Wówczas

$tg\ \alpha=\frac{\frac{12}{13}}{\frac{5}{13}}=\frac{12}{13}\cdot\frac{13}{5}=\frac{12}{5}$

Odpowiedź A.

200127

Rozwiązanie:

Skorzystajmy ze wzoru:

$sin^2\alpha+cos^2\alpha=1$

Obliczmy $cos^2\alpha$ .

$cos^2\alpha=1-sin^2\alpha=1-\bigg(\frac{\sqrt3}{2}\bigg)^2=1-\frac{3}{4}=\frac{1}{4}$

Obliczmy wartość wyrażenia:

$sin^2\alpha-3cos^2\alpha=\bigg(\frac{\sqrt3}{2}\bigg)^2-3\cdot\frac{1}{4}=\frac{3}{4}-3\cdot\frac{1}{4}=\frac{3}{4}-\frac{3}{4}=0$

Uwaga!
To nie są jedyne prawidłowe sposoby na rozwiązanie powyższych zadań. Istnieją inne sposoby o niekoniecznie wyższym stopniu trudności.

O MATHko!

Trenuj! – trygonometria cz. 1

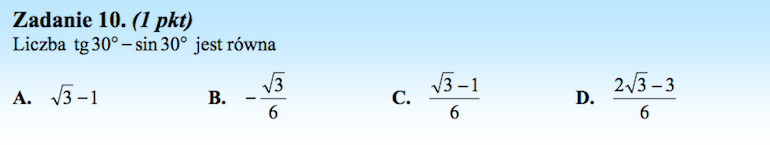
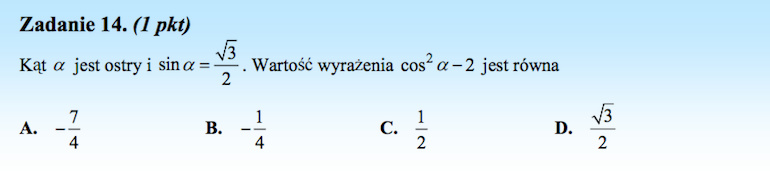
Dodaj komentarz Anuluj pisanie odpowiedzi