Trenuj! – równania i nierówności

Równania i nierówności, wśród zadań maturalnych, pojawiają się dość często. Warto zatem przejrzeć przykładowe zadania CKE dotyczące tego zagadnienia. W dużej części są to zadanie warte 1 punkt, ale pojawia się też zadanie otwarte. Ważne, aby pamiętać o wyznaczeniu dziedziny, bo od tego zależy wyznaczenie poprawnego rozwiązania równania.

Nie znajdziesz tu typowego zadania za 2 punkty, polegającego na rozwiązaniu nierówności kwadratowej. O nierówności kwadratowej możesz poczytać TUTAJ.

Zaczynamy!

Rozwiążmy równanie:

$x(x+3)-49=x(x-4)$

$x^2+3x-49=x^2-4x\ |-x^2$

$3x-49=-4x$

$3x+4x=49$

$7x=49\ |:7$

$x=7$

$7\in (2; +\infty)$
Odpowiedź D.

Rozwiążmy nierówność:

$\frac{3}{8}+\frac{x}{6}<\frac{5x}{12}\ \ \bigg|\cdot 24$

$24\cdot \frac{3}{8}+24\cdot \frac{x}{6}<24\cdot \frac{5x}{12}$

$3\cdot 3+4x<2\cdot 5x$

$9<10x-4x$

$9<6x$

$6x>9\ |:6$

$x>\frac{9}{6}$

$x>1\frac{1}{2}$

Odpowiedź B.

Rozwiążmy nierówność:

$\frac{x}{2}\leq \frac{2x}{3}+\frac{1}{4}\ \ \bigg|\cdot 12$

$12\cdot \frac{x}{2}\leq 12\cdot \frac{2x}{3}+12\cdot \frac{1}{4}$

$6x\leq 8x+3$

$-3\leq 8x-6x$

$-3\leq 2x\ |:2$

$-\frac{3}{2}\leq x$

$x\geq -\frac{3}{2}$

Odpowiedź B.

Rozwiążmy równanie:

$(2x-1)\cdot (x-2)=(1-2x)\cdot (x+2)$

$2x^2-4x-x+2=x+2-2x^2-4x$

$4x^2-2x=0$

$2x(2x-1)=0$

$x=0$ lub $2x-1=0$
Odpowiedź B.

Rozwiążmy nierówność:

$\frac{2-x}{3}-\frac{2x-1}{2}<x\ \bigg|\cdot 6$

$2\cdot(2-x)-3\cdot (2x-1)<6x$

$4-2x-6x+3<6x$

$7<6x+2x+6x$

$7<14x$

$14x>7\ |:14$

$x>\frac{1}{2}$

Odpowiedź D.

Wyznaczmy dziedzinę:
$D=\mathbb{R} \backslash \{-1\}$
Rozwiążmy równanie, skorzystajmy z własności proporcji:

$x-1=(x-1)(x+1)$

Rozważmy dwa przypadki:
$1)\ x\neq 1$

$x-1=(x-1)(x+1)\ |:(x-1)$

$1=x+1$

$x=0$

Drugi przypadek:
$2)\ x=1$
Wówczas dla równania
$x-1=(x-1)(x+1)$
mamy
$0=0$
Zatem $x=1$ także jest rozwiązaniem równania.
Odpowiedź D.

Pierwiastki równania, (czyli jego rozwiązania) to:

$x_1=-3, x_2=-7, x_3=11$

Zatem suma wszystkich rozwiązań wynosi:

$(-3)+(-7)++11=1$

Odpowiedź C.

Rozwiążmy nierówność:

$\frac{3}{5}-\frac{2x}{3}\geq \frac{x}{6}\ \ \bigg|\cdot 30$

$30\cdot \frac{3}{5}-30\cdot \frac{2x}{3}\geq 30\cdot \frac{x}{6}$

$18-20x\geq 5x$

$-20x-5x\geq -18$

$-25x\geq -18\ |:(-25)$

$x\leq \frac{-18}{-25}$

$x\in \bigg(-\infty,\frac{18}{25}\bigg>$

Odpowiedź B.

Z własności proporcji mamy:

$x(x+1)=(x-1)(5x-4)$

$x^2+x=5x^2-4x-5x+4$

$x^2-5x^2+x+9x-4=0$

$-4x^2+10x-4=0$

$a=-4, b=10, c=-4$

$\Delta=b^2-4ac=100-4\cdot (-4)\cdot (-4)=100-64=36$

$x_1=\frac{-10-6}{2\cdot (-4)}=\frac{-16}{-8}=2,\ \ x_2=\frac{-10+6}{2\cdot (-4)}=\frac{-4}{-8}=\frac{1}{2}$

Rozwiązanie:

$x\in \left\{\frac{1}{2},2 \right\}$

Dziedzina
$D=\mathbb{R} \backslash \{3\}$
Skorzystajmy z własności proporcji:

$3\cdot(2x-4)=4\cdot (3-x)$

$6x-12=12-4x$

$6x+4x=12+12$

$10x=24\ |:10$

$x=\frac{24}{10}=\frac{12}{5}$

Odpowiedź B.

O MATHko!

Trenuj! – równania i nierówności

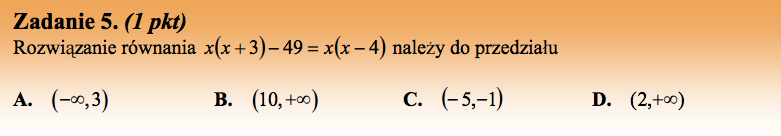
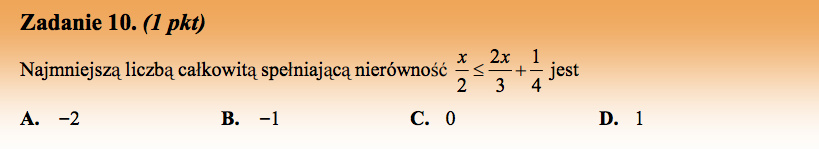
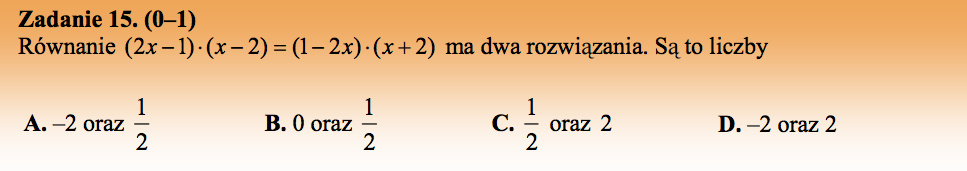
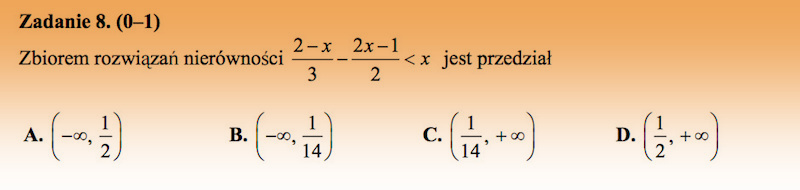
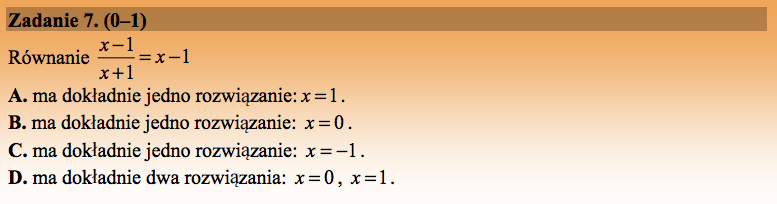
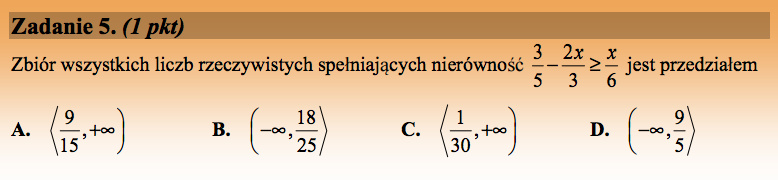
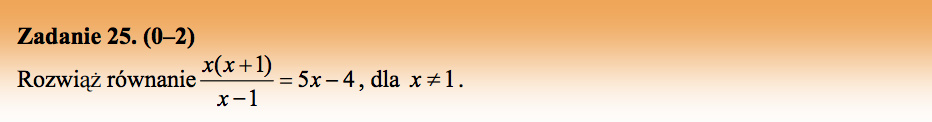
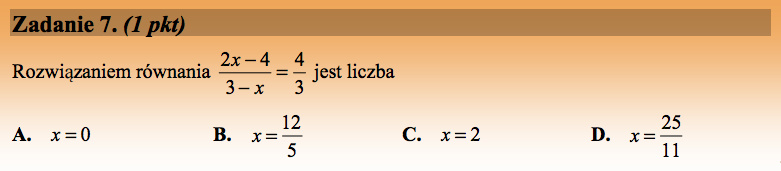
Dodaj komentarz Anuluj pisanie odpowiedzi