Pierwszą część zadań maturalnych z zakresu równania i nierówności znajdziesz tutaj. Tymczasem rozważymy kilka równań i nierówności różnych typów z najnowszych arkuszy Centralnej Komisji Egzaminacyjnej. Do dzieła!
Jeśli masz do czynienia z równaniem danym w postaci iloczynowej, sprawdź czy prawa strona jest równa zero. Wówczas sprawa jest prosta. Iloczyn jest równy zero, jeśli którykolwiek z czynników wynosi zero. Zatem:
![]() lub
lub ![]() lub
lub ![]() .
.
Pierwszy czynnik, to już gotowe rozwiązanie. Drugi czynnik ma dwa rozwiązania:
![]()
wtedy, gdy
![]()
zatem
![]() lub
lub ![]() .
.
Trzeci czynnik, to równanie sprzeczne. Kwadrat liczby rzeczywistej nie może być ujemny. Nasze równanie ma trzy rozwiązania.
Odp.: C
Podczas, gdy w poprzednim przypadku milcząco przyjąłeś, że zbiór wszystkich możliwych rozwiązań równania zawiera się w zbiorze liczb rzeczywistych, teraz musisz na początku wyznaczyć dziedzinę równania. O tym, że nie dzieli się przez zero wiesz od czasów wczesnej podstawówki. Zatem w mianowniku nie może pojawić się zero:
![]() ,
,
czyli dziedzina, to zbiór liczb rzeczywistych oprócz 2 i -2.
![]()
Teraz wystarczy zauważyć, że ułamek jest równy zero, jeśli licznik jest równy zero, czyli:
![]() . Zauważ, że:
. Zauważ, że:
![]() .
.
Zatem licznik zeruje się dla
![]() oraz
oraz ![]()
Ponieważ ![]() nie należy do dziedziny, rozwiązanie jest jedno, równe zero.
nie należy do dziedziny, rozwiązanie jest jedno, równe zero.
Odp.: D
Przyjrzyjmy się lewej stronie równości dla konkretnych wartości x:
![]() dla
dla ![]() mamy
mamy ![]()
![]() dla
dla ![]() mamy
mamy ![]()
![]() dla
dla ![]() mamy
mamy ![]()
Odp.: C
Iloczyn jest równy zero, jeśli którykolwiek z czynników wynosi zero. Zatem
![]() lub
lub ![]()
wówczas
![]() lub
lub ![]()
Pierwsze równanie posiada jedno rozwiązanie w zbiorze liczb rzeczywistych, a drugie – dwa rozwiązania:
![]() lub
lub ![]() lub
lub ![]()
Odp.: ![]() .
.
Rozważmy nierówność liniową:
![]()
![]()
![]() .
.
Przy dzieleniu nierówności przez liczbę ujemną zmieniamy znak nierówności:
![]()
Rozwiązaniem nierówności są wszystkie liczby mniejsze bądź równe ![]()
Odp.: D
Mnożymy nierówność przez 6 – najmniejszą wspólną wielokrotność liczb 2 i 3:
![]()
![]()
![]()
![]()
![]()
Dzielimy nierówność przez liczbę ujemną, zmieniamy znak:
![]()
Zbiorem wszystkich rozwiązań nierówności są liczby mniejsze od ![]() .
.
Odp.: A
Zadanie zamknięte nie wymaga znalezienia pełnego zbioru rozwiązań nierówności. Wystarczy sprawdzić, które liczby spośród proponowanych spełniają nierówność:
![]()
Dla ![]() mamy
mamy ![]()
Dla ![]() mamy
mamy ![]()
Dla ![]() mamy
mamy ![]()
Dla ![]() mamy
mamy ![]()
Odp.: D
Nierówność kwadratowa, to zadanie-pewniak na egzaminie maturalnym z matematyki. Schemat rozwiązania przykładowej nierówności znajdziesz tutaj. Tym razem podejdziemy do zagadnienia nieco inaczej, to znaczy „bez delty”.
Na początek rozważ równanie:
![]()
![]()
![]() lub
lub ![]()
![]() lub
lub ![]()
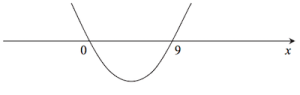
Drugi etap, to znalezienie rozwiązań nierówności ![]()
na przykład w oparciu o pomocniczy wykres:
Zapisujemy zbiór rozwiązań nierówności
![]()
lub w postaci przedziału domkniętego:
![]()
i już! 😀
Sprawdź jakie pułapki czyhają na rozwiązujących równania i nierówności kwadratowe.
Źródło:
https://cke.gov.pl/egzamin-maturalny/


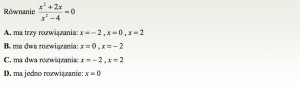



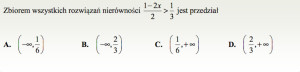
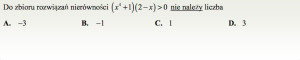

Dodaj komentarz