Trenuj! – prawdopodobieństwo

Dzisiaj bierzemy na tapetę zadania egzaminacyjne z rachunku prawdopodobieństwa (poziom podstawowy). Dział nietrudny, bardzo intuicyjny i lubiany przez (niektórych) maturzystów. Zaczynamy!

Jeśli potrzebujesz teoretycznego wsparcia zajrzyj TUTAJ.

W rzucie symetryczną kostką mamy 6 możliwych wyników doświadczenia – wszystkie równie prawdopodobne.

$\{1, 2, 3, 4, 5, 6\}$

Gdy rzucamy dwiema kostkami możliwych jest 36 wyników doświadczenia.

$\{(1,1),(1,2),(1,3),(1,4),(1,5),(1,6), (2,1),(2,2),...,(6,5),(6,6)\}$

Jeśli rozważamy zdarzenie polegające na tym, że iloczyn wyrzuconych oczek wynosi 5, wówczas mamy dwa możliwe wyniki sprzyjające temu zdarzeniu
$(1,5),(5,1)$ .
Prawdopodobieństwo to iloraz liczby zdarzeń sprzyjających i liczby wszystkich możliwych zdarzeń:

$p=\frac{2}{36}=\frac{1}{18}$

Odpowiedź: B

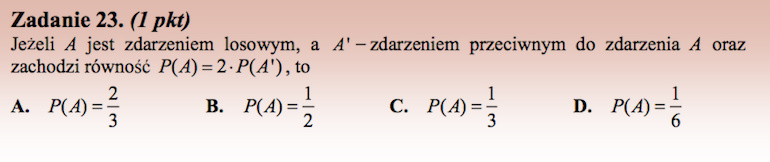
Jeśli rozważamy zdarzenie losowe A i A’ – zdarzenie przeciwne do A, to należy pamiętać, że:

$P(A)+P(A')=1$

czyli

$P(A')=1-P(A)$

Zatem, jeśli

$P(A)=2\cdot P(A')$

wówczas

$P(A)=2\cdot (1-P(A))$

$P(A)=2-2\cdot P(A)$

$P(A)+2\cdot P(A)=2$

$3\cdot P(A)=2\ |:3$

$P(A)=\frac{2}{3}$

Odpowiedź: A

Jeśli mamy dziesięciu zawodników, spośród których wybieramy dwóch graczy, to pierwszego z nich wybierzemy na 10 sposobów (jeden z dziesięciu), a drugiego na 9 sposobów (jeden z pozostałych dziewięciu). Stosujemy regułę mnożenia $10\cdot 9 =\ldots$
Odpowiedź: B

Liczby podzielne przez $4$ to $4,8,12$ .
Ponieważ zbiór, z którego wybieramy liczbę ma 15 elementów, to:
$p=\frac {3}{15}=\frac{1}{5}$
Odpowiedź B.

$\Omega = \{(1,1),(1,2),(1,3),(1,4),(1,5)\ldots (8,7),(8,8)\}$
$|\Omega |=64$
$A=\{(5,1), (6,2), (7,3),(8,4),(7,1),(8,2)\}$
$|A|=6$

$P(A)=\frac{|A|}{|\Omega|}=\frac{6}{64}=\frac{3}{32}$

$\Omega = \{(1,1),(1,2),(1,3),(1,4),(1,5)\ldots (6,5),(6,6)\}$
$|\Omega |=36$
$|A|=\{(1,2), (2,1)\}$
$P(A)=\frac{|A|}{|\Omega|}=\frac{2}{36}=\frac{1}{18}$
Odpowiedź D.

Przypomnijmy, czym jest prawdopodobieństwo sumy dwóch zdarzeń

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

Ponieważ zdarzenia A i B się wykluczają

$A\cap B=\emptyset$

to prawdopodobieństwo jest równe

$P(A\cap B)=P(\emptyset )=0$

Zatem

$P(A\cup B)=P(A)+P(B)$

$P(B)=1-P(B')=1-0,4=0,6$

$P(A\cup B)=P(A)+P(B)=0,3+0,6=0,9$

Odpowiedź D.

Pierwszy kolor – wybieramy 1 z 10 – mamy 10 możliwości wyboru.
Drugi kolor – 1 z 9 – pasy leżące obok muszą być innego koloru – 9 możliwości.
Trzeci kolor – tu wyboru nie ma, kolor został wybrany przy pierwszym podejściu.
Stosujemy regułę iloczynu i otrzymujemy liczbę możliwych do uszycia flag:
$10\cdot 9\cdot 1=90$ .
Odpowiedź C.

$\Omega = \{(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(1,7),(2,1)\ldots (7,6),(7,7)\}$
$|\Omega |=7\cdot 7=49$
$A=\{(1,2),(1,5), (2,1),(2,4),(2,7), (3,3),(3,6), (4,2),(4,5), (5,1),(5,4),(5,7), (6,3),(6,6), (7,2),(7,5)\}$
zatem $|A|=16$

$P(A)=\frac{|A|}{|\Omega|}=\frac{16}{49}$

100031

$\Omega = \{(1,1),(1,2),(1,3)\ldots (7,7)\}$
$|\Omega |=7\cdot 7=49$
$A=\{(1,6), (2,3),(2,6), (3,2),(3,4),(3,6), (4,3),(4,6), (5,6), (6,1),(6,2),(6,3),(6,4),(6,5),(6,6),(6,7),(7,6)\}$
$|A|=17$

$P(A)=\frac{|A|}{|\Omega|}=\frac{17}{49}$

O MATHko!

Trenuj! – prawdopodobieństwo

Dodaj komentarz Anuluj pisanie odpowiedzi