Nie zdam.
Chyba nie zdam.
Nie ma szans, żebym zdał.
Od studniówki te słowa są odmieniane przez (prawie) każdego maturzystę. Znam wielu, którzy negatywnie się nastawiają. Zupełnie niesłusznie, bo na jakiej podstawie? Czy mamy wystarczającą ilość danych, aby wyrokować?
PRAWDOPODOBNIE nie 😉
Dwa wyniki – zdam/nie zdam – 50% szans. Ale czy na pewno? Czy wszystkie czynniki mające wpływ na wynik zostały uwzględnione? Czy jesteśmy w stanie oszacować wszystkie czynniki? To dość trudne, ale z prognozami nie jest łatwo. Można się o tym przekonać sprawdzając prognozę pogody – te dwudziestoczterogodzinne sprawdzają się najczęściej. Zatem na dzień przed maturą, można już z dużym prawdopodobieństwem obstawić wynik egzaminu ZDAM/NIE ZDAM.
Zacznijmy od podstaw. Czym jest prawdopodobieństwo i jak je obliczyć?
Oto kilka podstawowych pojęć, bez których ani rusz:
DOŚWIADCZENIE LOSOWE to np. rzut kostką, rzut monetą, dwukrotny rzut monetą, itd.
ZDARZENIE ELEMENTARNE – pojedynczy wynik doświadczenia losowego, na przykład:
- w rzucie kostką wypadło jedno oczko,
- w trzykrotnym rzucie monetą za każdym razem wypadł orzeł: (O, O, O).
ZDARZENIE LOSOWE – podzbiór zdarzeń elementarnych, czyli zbiór możliwych wyników doświadczenia losowego, na przykład:
- w rzucie kostką wypadła parzysta liczba oczek {2, 4, 6},
- w rzucie dwiema kostkami suma wyrzuconych oczek wynosi 7:
{(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}, - w trzykrotnym rzucie monetą za pierwszym razem wypadł orzeł:
{(O, R, R), (O, R, O), (O, O, R), (O, O, O)}.
Zdarzenia losowe oznaczamy wielkimi literami alfabetu: ![]() .
.
ZDARZENIE PRZECIWNE do zdarzenia losowego ![]() oznaczamy
oznaczamy ![]() .
.
Jeśli rozważamy następujące zdarzenie losowe w rzucie monetą wypadła reszka, to zdarzeniem przeciwnym jest wypadnięcie orła:
![]() ,
, ![]()
Jeśli doświadczenie losowe polega na dwukrotnym rzucie monetą i rozważamy zdarzenie losowe
w dwukrotnym rzucie monetą wypadły dokładnie dwie reszki, czyli:
![]() wówczas
wówczas ![]()
Zbiór wszystkich zdarzeń elementarnych oznaczamy grecką wielką literą ![]() (omega).
(omega).
MOC ZBIORU to liczba elementów tego zbioru.
Moc zbioru wszystkich zdarzeń elementarnych (moc zbioru omega) oznaczamy ![]() .
.
Inne spotykane oznaczenia to ![]() lub
lub ![]() .
.
- W rzucie kostką
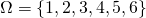 ,
, 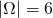 ,
, - W rzucie monetą
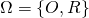 ,
, 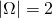 ,
, - W dwukrotnym rzucie monetą
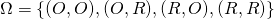 ,
, 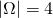 ,
,
To był wstęp. Teraz istota sprawy 🙂
Prawdopodobieństwo zdarzenia losowego ![]() to iloraz liczby zdarzeń sprzyjających przez liczbę wszystkich zdarzeń:
to iloraz liczby zdarzeń sprzyjających przez liczbę wszystkich zdarzeń:
![]()
Jeśli ![]() , to
, to ![]() nazywamy zdarzeniem niemożliwym.
nazywamy zdarzeniem niemożliwym.
Jeśli ![]() , to
, to ![]() nazywamy zdarzeniem pewnym.
nazywamy zdarzeniem pewnym.
UWAGA: Prawdopodobieństwo zdarzenia zawsze przyjmuje wartość z przedziału ![]() .
.
Własności:
![]()
![]()
![]()
![]()

Dodaj komentarz