Trenuj! – własności funkcji

Funkcje nie są ulubionym tematem maturzystów, jednak na poziomie podstawowym, możemy podejść do tematu bez potknięć. Gotowi? Start!

Miejsce zerowe funkcji, to taki argument funkcji $(x_0)$ , dla którego wartość funkcji $f(x_0)$ , wynosi zero:
$f(x_0)=0$
Z drugiej strony, jeśli liczba 1 jest miejscem zerowym funkcji, to punkt (1,0) należy do jej wykresu.
Jeśli dwa punkty
$P_1=(x_1, y_1)$ oraz $P_2=(x_2,y_2)$
należą do wykresu funkcji liniowej, to jej współczynnik kierunkowy najszybciej obliczymy ze wzoru:

$a=\frac{y_2-y_1}{x_2-x_1}$

Zatem
punkty $M=(3,-2)$ oraz $P =(1,0)$ należą do wykresu funkcji stąd mamy

$a=\frac{0-(-2)}{1-3}=\frac{2}{-2}=-1$

Odp.: D

Wyznaczmy argument funkcji, dla którego wartość wynosi zero
$\sqrt3(x+1)-12=0$
$x\sqrt3+\sqrt3-12=0$
$x\sqrt3=12-\sqrt3\ |:\sqrt3$

$x=\frac{12-\sqrt3}{\sqrt3}=\frac{\sqrt3(\cdot12-\sqrt3)}{\sqrt3\cdot \sqrt3}=\frac{12\sqrt3-3}{3}=\frac{3\cdot(4\sqrt3-1)}{3}=4\sqrt3-1$

Odp.: C

Funkcja liniowa $f(x)=ax+b$ jest:
rosnąca, gdy $a>0$
malejąca, gdy $a<0$
stała, gdy $a=0$ .
W naszym przypadku

$a=\frac{1}{3}>0$

zatem funkcja jest rosnąca.
Z kolei punkt przecięcia funkcji liniowej $f(x)=ax+b$ z osią $OY$ , to punkt $(0,b)$ .
Nasza funkcja ma postać
$f(x)=\frac{1}{3}x-1$
zatem

$b=-1$

stąd punkt przecięcia z osią $OY$ , to $P=(0,-1)$ .
Odp.: D

Postać iloczynowa funkcji kwadratowej wygląda następująco $f(x)=a(x-x_1)(x-x_2)$ ,
$x_1, x_2$ to miejsca zerowe tej funkcji.
W naszym przypadku $x_1=-3$ , $x_2=5$ stąd

$x_1+x_2=-3+5=2$

Odp.: C

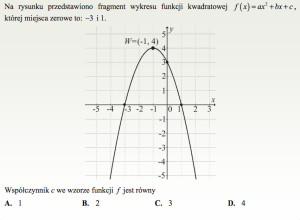
Aby wyznaczyć współczynnik $c$ , wystarczy odczytać z wykresu punkt przecięcia z osią $OY$ . Ten punkt, to $P=(0,3)$ , zatem $c=3$ .
Odp.: C

Jeśli dany jest wzór funkcji kwadratowej w postaci ogólnej, tzn. $f(x)=ax^2+bx+c$ , to wierzchołek wykresu funkcji $W=(p,q)$ obliczymy ze wzorów:

$p=-\frac{b}{2a}$

$q=-\frac{\Delta}{4a}$

gdzie
$\Delta=b^2-4ac$
Zatem, jeśli mamy wzór funkcji $f(x)=x^2-6x-3$ , to
$a=1$
$b=-6$
$c=-3$
i wówczas

$p=-\frac{-6}{2\cdot 1}=\frac{6}{2}=3$

$\Delta=(-6)^2-4\cdot 1\cdot (-3)=36+12=48$

$q=-\frac{48}{4}=-12$

Zatem wierzchołkiem wykresu jest punkt $W=(3,-12)$ .
Odp.: C

To zadanie otwarte, wybierzmy najszybszą możliwą drogę do znalezienia rozwiązania.
Jeśli funkcja przyjmuje tę samą wartość dla $x=-6$ oraz $x=0$ , to znaczy, że oś symetrii wykresu funkcji znajduje się dokładnie w równej odległości między tymi punktami. A oś symetrii wykresu, to jednocześnie pierwsza współrzędna wierzchołka paraboli:

$p=\frac{-6+0}{2}=-3$

Przypomnijmy sobie postać kanoniczną funkcji kwadratowej, wykorzystującą wierzchołek paraboli $W=(p,q)$

$f(x)=a(x-p)^2+q$

Ponieważ największa wartość funkcji to $6$ , czyli współrzędne wierzchołka to $(-3,6)$ . Ponadto znamy jeden z punktów należących do wykresu funkcji $(0,\frac{3}{2})$ . Zatem

$\frac{3}{2}=a(0+3)^2+6$

$\frac{3}{2}=9a+6$

$9a=\frac{3}{2}-6$

$9a=-4,5 \ |:9$

Odp.:

$a=-\frac{1}{2}$

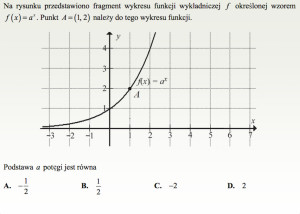Jeśli punkt $A=(1,2)$ należy do wykresu funkcji $f(x)=a^x$ , to spełnia jej równanie, zatem:
$a^x=f(x)$
$a^1=2$
$a=2$
$f(x)=2^x$
Odp,: D

$a^x=f(x)$
$a_2=9$
$a=\sqrt 9$
$a=3$
$f(x)=3^x$
Zbiór wartości funkcji wykładniczej $f$ , to zbiór liczb dodatnich: $(0;\infty)$
Wykres funkcji $g$ , to wykres funkcji $f$ przesunięty o dwie jednostki w dół, zatem
$Zw_g =(-2,\infty)$ .

Źródło:
https://cke.gov.pl/egzamin-maturalny/

O MATHko!

Trenuj! – własności funkcji

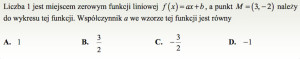
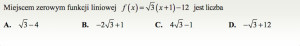
Dodaj komentarz Anuluj pisanie odpowiedzi